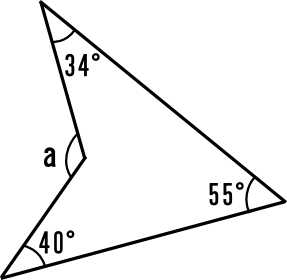
2－4－1 星型多角形の内角の和 教材（問題場面） ※m 点とばし星型n 角形の内角の和は180°×（n－2－2m）と表すことができる。 180° 360° 540° 7° 900° 1080° 1260° 1440° 180° 180° 180° 360° 360° 360° 540° 540° 7° 内角の和・外角の和の証明 なぜn角形の内角の和が180°×（n2）となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習になります。向かい合う角の和は180° 円に内接する四角形における一番有名な性質です。 180^ {\circ} 180∘ である。 つまり， 性質1の逆も成立します。 つまり， 向かい合う内角の和が 180^ {\circ} 180∘ である四角形は円に内接します。 また，性質1は「外角」を使って
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
動物イラストa4サイズ サイコロ展開図 サイコロを10パターン用意しました。展開図になっているのでプリントしてお使い下さい。さいころの展開図 難易度は上級レベル～です。 さいころ（立方体）の見えている面から裏面を推理するなど、展開図から考える問題集です。 受験では定番ですが、ペーパーでの問題は難易度が高くなってきます。 しっかり実体験を積んだうえ、問題にこのピンは、Yoriko Utsunomiyaさんが見つけました。あなたも で自分だけのピンを見つけて保存しましょう！
無料イラスト サイコロの展開図 透過png
③四角形の内角の和は360°になることを演繹的に考え、説明する。 児童の学習活動 ・教師の働きかけ 例題1：2本の対角線で分ける。 を基に説明の仕方を考える。 つに分かれるのに、なぜ四角 形の内角の和は360°になるのか理由を 考えさせる。め，内角の和が180°ずつ増えていく。つまり， 角形の内角の和）×（三角形の個数）」ととらえ ることもできる。 ここで，星型多角形（1点とばし）についても 演繹的な説明を考えてみる。 ①n角形の外角の和を利用する 星型n角形の角の和は内角の和・外角の和の証明 なぜn角形の内角の和が180°×（n2）となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習にな
中学２年数学練習問題 図形の調べ方 多角形の内角と外角の解答
(1) 図形の性質に関心をもち，三角形や四角形の角の大きさの和について，筋道を立てて考えようとし ている。 算数への関心・意欲・態度 (2) 三角形の3つの角の大きさの和が180°であることを帰納的に見いだし，四角形の4つの角の大きまた，角については2 本の半直線が作る平面図形としての角を定義し，2 つの辺の開き具合によって形が違うなど，形としての角の概念について基本的なことを学習して きた。第4 学年では，回転による反直線の開きの量としての角を扱っている。また，四角形につ いては，台形，平行四辺形 図形の角の大きさ 5年生 三角形の内角の和が180°であることをもとに、三角形や四角形の示されていない角の大きさを求める問題にチャレンジしていました。
多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
七夕飾りの星の作り方：折り紙で簡単に作る星飾り3パターン！ 更新日 17年12月8日 季節のイベント 今回はトク娘が七夕飾りの星の作り方を3パターン解説します！ 七夕は、星に関
正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 （頂点の数）＝（面の頂点の数）×（面の数）÷（1点に集まる面の数） たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の
