正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の
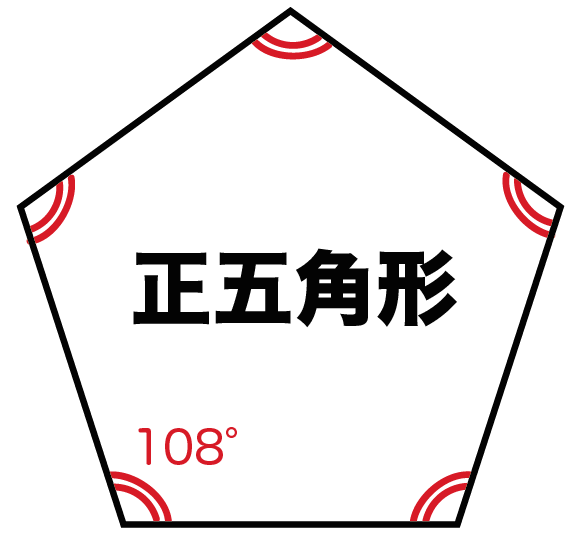
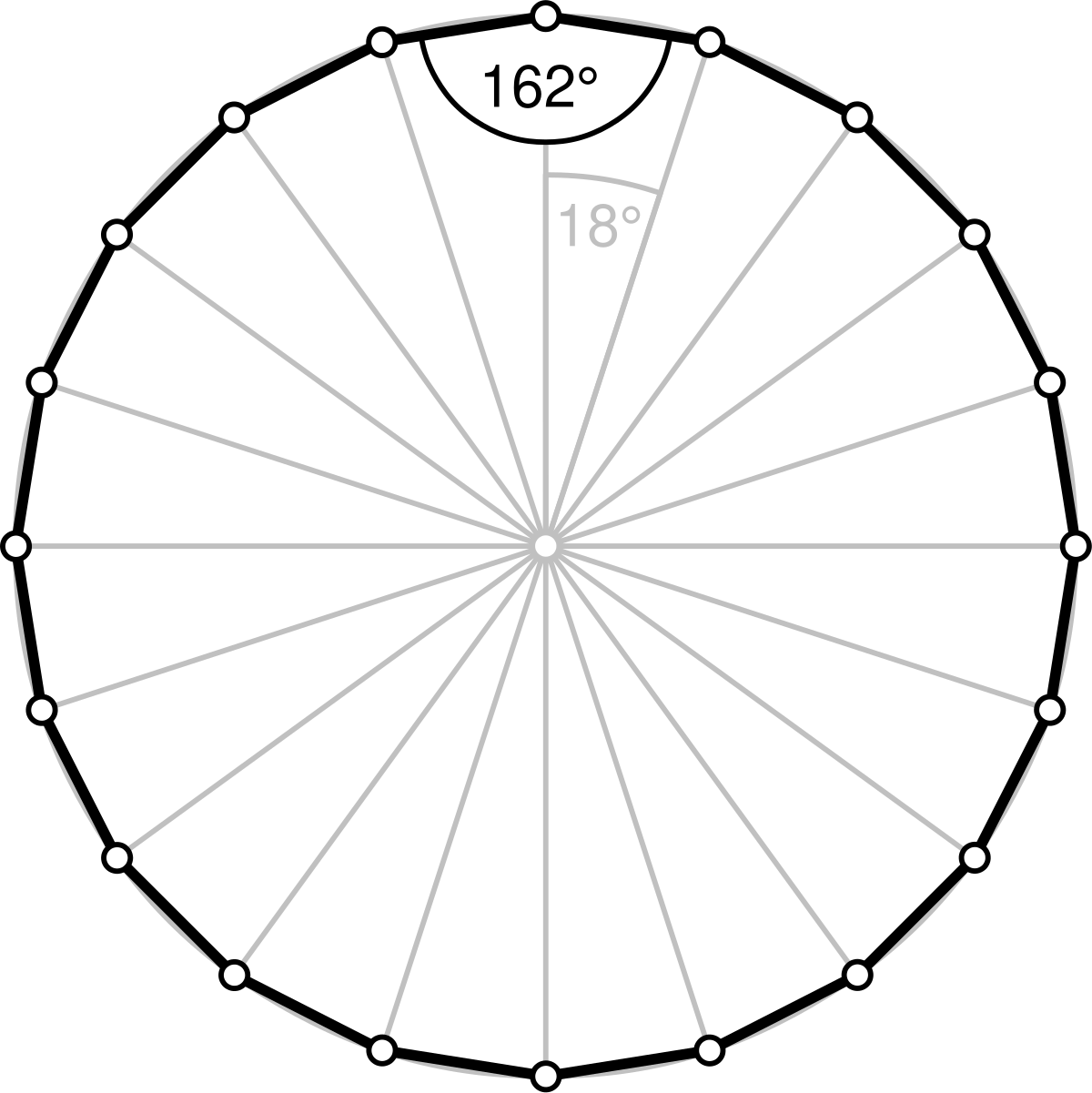
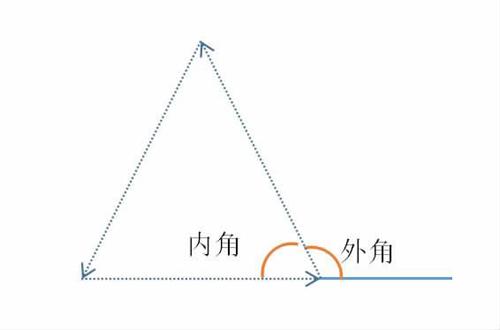
正多角形 内角 公式- 多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。 推论 n边形的内角和公式为(n-2)×180°(n大于等于3且n为整数)。 任意正多边形的外角和=360° 正多边形任意两条相邻边连线所构成的三角形是等腰三角形 多边形内角和定理证明 正多角形の内角(外角)の求め方とは 正多角形とは、 「すべての辺の長さが等しく、すべての内角の大きさが等しい多角形」 を指します。 よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます
正多角形 内角 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  | |
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  | |
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  |  |
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 | ||
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 | ||
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 | ||
「正多角形 内角 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
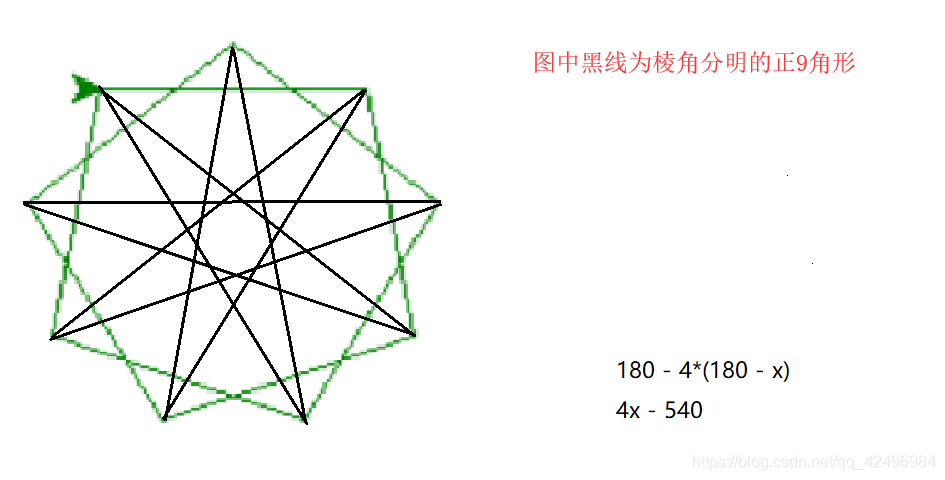
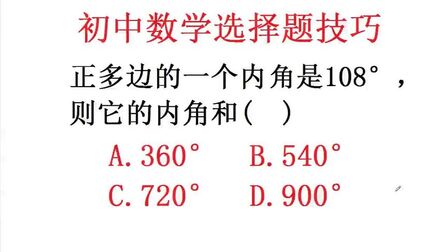
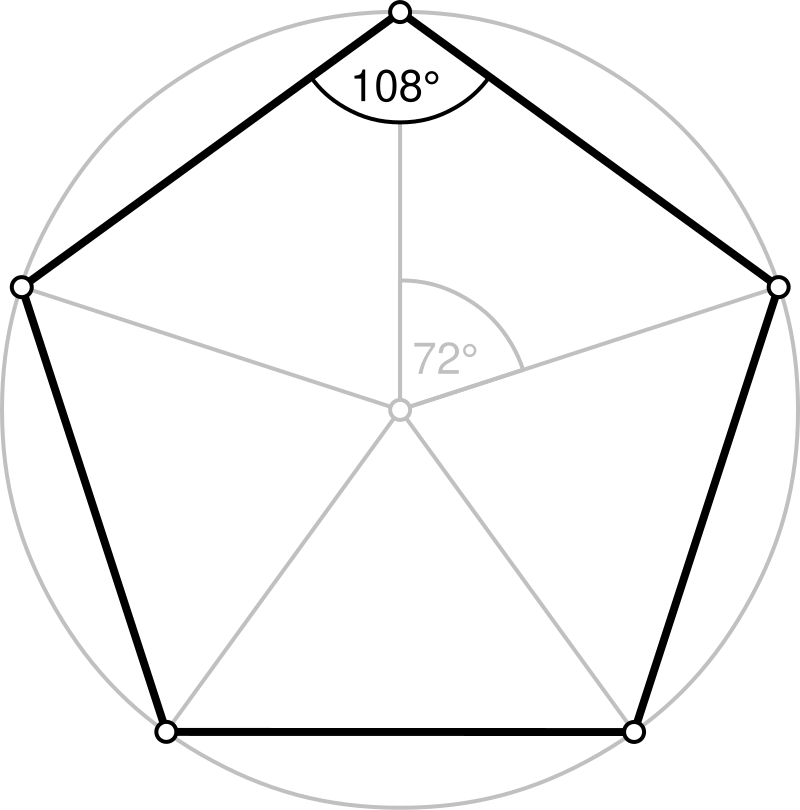
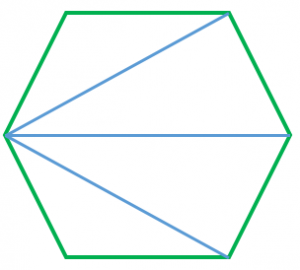
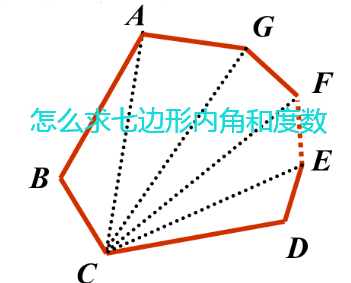
5角形の内角の和は 180°×3=540° すべての辺の長さが等しく,すべての内角の大きさが等しい多角形を 正多角形 という • 多角形の外角の和は 360° 正多角形のすべての内角の大きさは等しく,すべての外角の大きさは等しい 180°× (n−2) 正多角形の面積公式一覧と導出方法を解説正二十四角形まで 21年12月4日 1辺の長さaの正方形の面積は、もちろん\ (a^2\)ですが、正三角形の面積公式は知っていますか 中学や高校の試験で登場するため、正三角形の面積公式は覚えておいて損はあり
Incoming Term: 正多角形 内角 公式,




0 件のコメント:
コメントを投稿