面積を求めよ。 次の問いに答えよ。 半径2cm,弧の長さ3πcmのおうぎ形の面積を求めよ。 半径6㎝、弧の長さ 10 3 π㎝のおうぎ形がある。面積を求めよ。 半径3cm弧の長さ5πcmのおうぎ形の面積を求めよ。 半径9cm,面積9πcm 2 のおうぎ形がある。 中心角を求めよ。 下の図の色の付いた部分の面積を求めなさい。ただし円周率は314する。 解説 下の図のように図形を分けて、考えます。 分けた後の図形の色の付いた部分は4分の1の円の面積(中心角90°のおうぎ形)から直角二等辺三角形の面積を引けば求めることができます。扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角（単位「度」）を
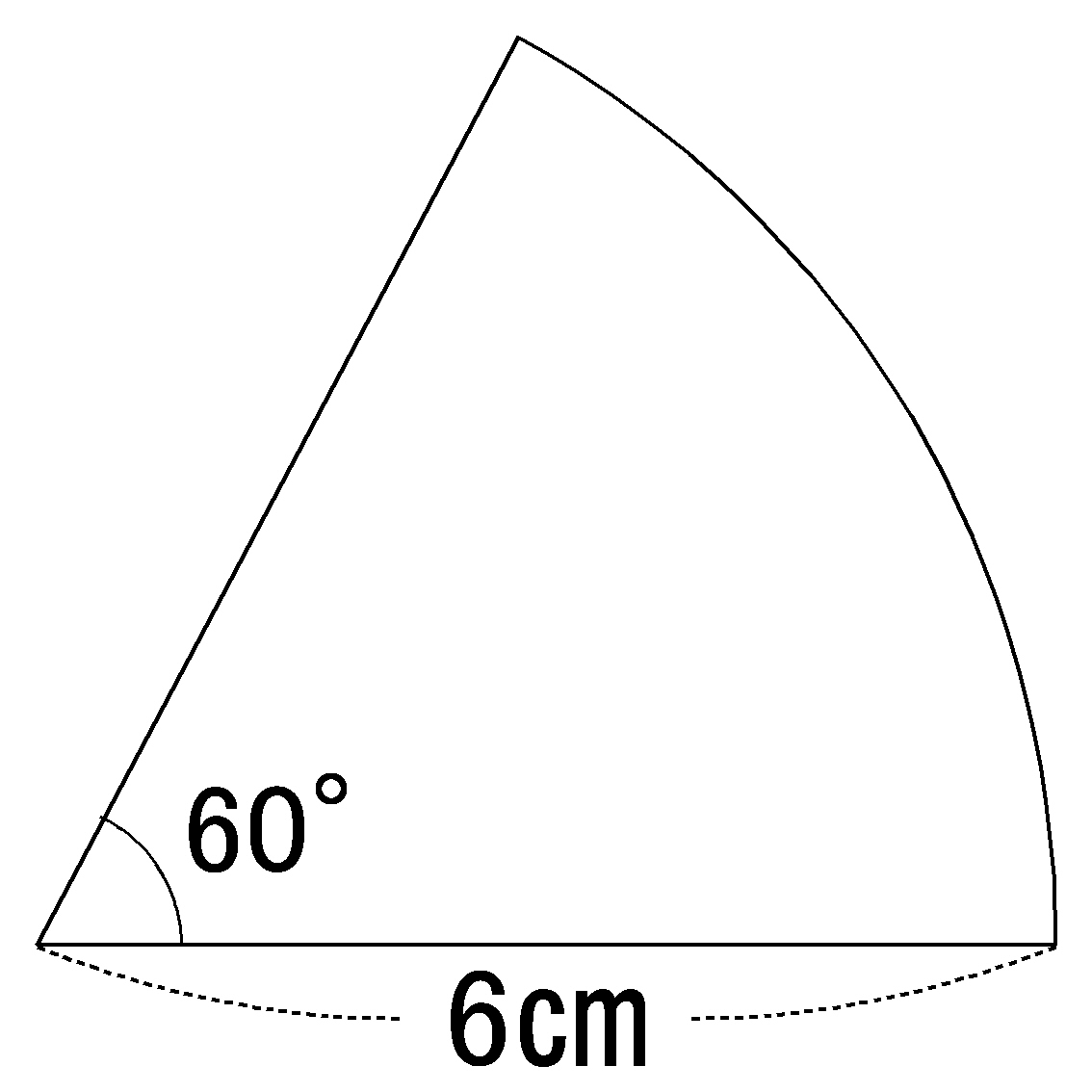
Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう
円とおうぎ形⑺ 正三角形が関係する問題 6 6 次の図は、1辺の長さが6㎝の正三角形と半円を組み合わせた図形です。 色のついた部分の面積を求めなさい。ただし円周率は314とします。 おうぎ形を含む図形の面積の難問。 今回は、小学生向けの図形の計量の難問を考えてみます。 上の図の濃く塗られた部分の面積を求めます。 まずは、左の図から。 円を元にして描いた、同じ図形が3つ組み合わせされた図形であることは、すぐに見ておうぎ形の面積の求め方1 おうぎ形ABCが存在する時に扇形の面積をSとすると、この面積Sを求める公式は次の (1)式のようになります。 S= 1 2(半径AB)(弧BC) (1) (1) S = 1 2 ( 半 径 A B) ( 弧 B C) この時の比較として三角形DEFも置いておきます。 三角形の面積を求める公式はもちろん 1 2( 1 2 ( 底辺)() ( 高さ)) となります。 1つ目の面積の求め方はおうぎ形を分割していくことに
Studydoctorおうぎ形の公式と忘れない考え方 中学１年数学 Studydoctor
中学1年生数学記事一覧 中学2年生数学記事一覧 算数円柱の体積の求め方！公式で確認～小学生向け～ 算数 時間・分・秒を変換計算式はどうやる？公式をご紹介！ 算数 116 中学入試問題つるかめ算の演習問題に挑戦！ 算数 130 立方体の体積小学生 小学生が理解する割合計算の教え方を伝授します！ 算数が苦手に感じてくるのは小学5年生が分岐点と言われます。 小学5年生の時に割合という算数が入ってきてここで引っかかる子も多いようです。 小学校のうちでなんだかわからないと割合の求め方 割合を表すのに，百分率 ひゃくぶんりつ （％）を使うことがあります。 百分率では，001倍のことを 1％（1パーセント）といいます。 また，割合を表すのに，歩合 ぶあい を使うこともあります。 割合を表す小数 1 01 001 0001 百分率 100% 10% 1% 01% 歩合 10割 1割 1分 1厘 割合を
割合 小学５年 割合の定義 算数の教え方教えますmother S Math Happy Study Support
