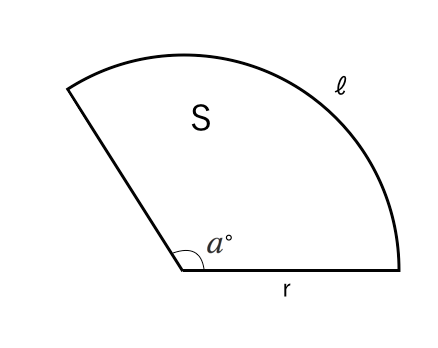
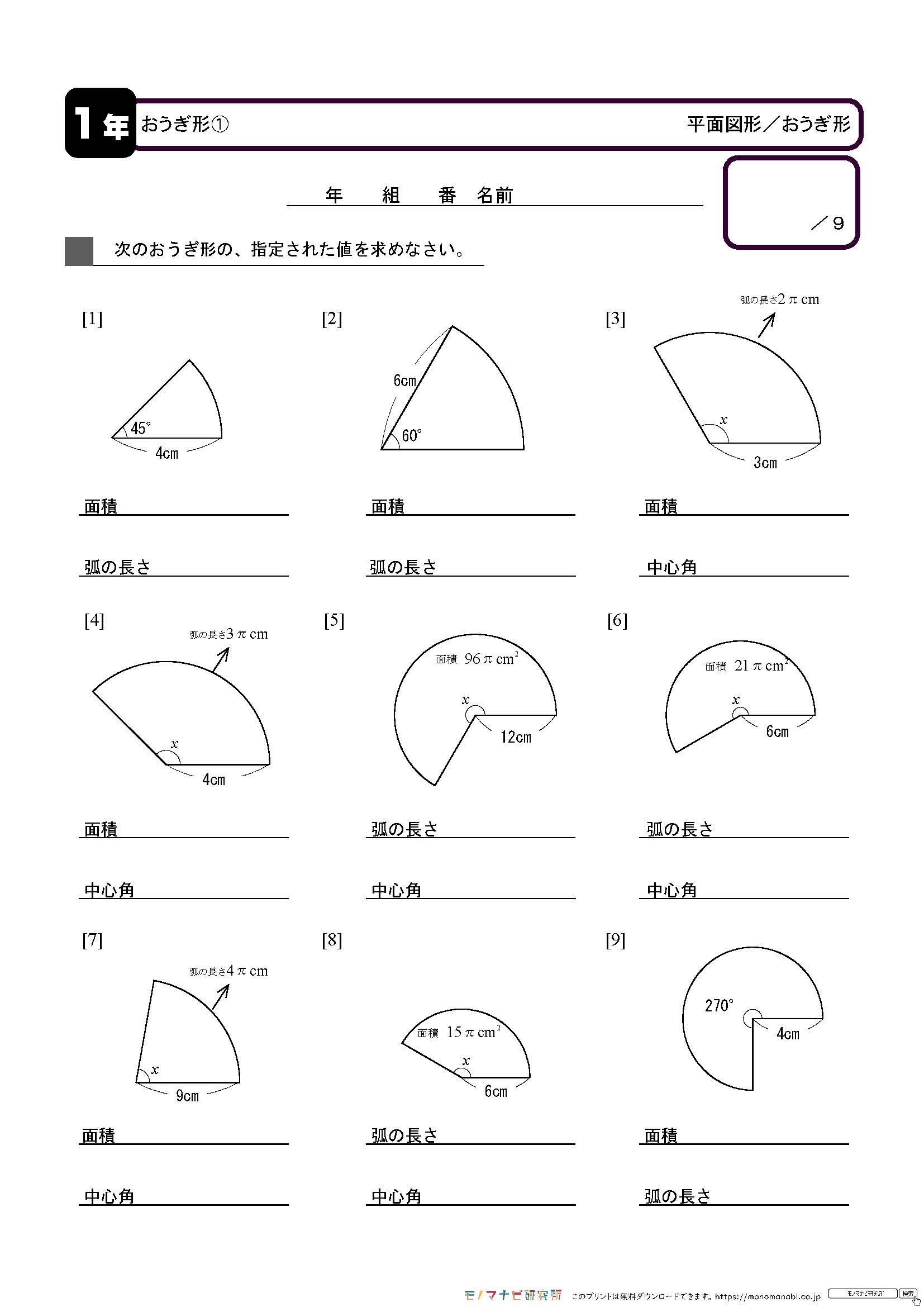
面積を求めよ。 次の問いに答えよ。 半径2cm,弧の長さ3πcmのおうぎ形の面積を求めよ。 半径6㎝、弧の長さ 10 3 π㎝のおうぎ形がある。面積を求めよ。 半径3cm弧の長さ5πcmのおうぎ形の面積を求めよ。 半径9cm,面積9πcm 2 のおうぎ形がある。 中心角を求めよ。 下の図の色の付いた部分の面積を求めなさい。ただし円周率は314する。 解説 下の図のように図形を分けて、考えます。 分けた後の図形の色の付いた部分は4分の1の円の面積(中心角90°のおうぎ形)から直角二等辺三角形の面積を引けば求めることができます。扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を
Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう
おうぎ形 面積
おうぎ形 面積- まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形のHello School 算数 円とおうぎ形 練習問題 解答と解説 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。 ※円周率はすべて314とする。



ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア
面積 S = πr2 × a 360 例半径18cm, 中心角40°のおうぎ形 弧の長さ=36π× 40 360 =4π (cm) 面積=324π× 40 360 =36π (cm2) 例題動画 半径と中心角から面積・弧を求めるおうぎ形の面積は,中心角が30度ですから,円の = になるので, 360 12 2)です。 よって,おうぎ形が通過した部分の面積は,162+8478=(cm2) になります。 はじめ おわり 18cm 18cm 18cm 18cm 30° 30° 18cm 18cm 18cm 30° 30° 18cm 高さ 18cm 18cm 30° 30° 18cm 高さ面積を求めよ。 半径28cm, 面積294πcm 2 のおうぎ形がある。 中心角を求めよ。 弧の長さを求めよ。 半径8cm, 面積 24 5 πcm 2 のおうぎ形がある。 中心角を求めよ。 弧の長さを求めよ。 弧の長さ14πcm, 中心角105°のおうぎ形がある。 半径を求めよ。 面積を求めよ。
答え おうぎ形の面積が与えられているので こちらの公式を利用します。 まずは、半径9㎝の円の面積を求めます。 そして、公式にそれぞれの値をあてはめていくと 約分をしていきましょう。 (πも約分で消えてしまいます) (2)半径 ㎝、弧の長さ cmのおうぎ形,立体の表面積・体積 ⑥ 次のおうぎ形の弧の長さと面積を求めな さい。 (1) 半径6cm,中心角60°のおうぎ形 次のおうぎ形の中心角の大きさを求めな さい。 (1) 半径5cm,弧の長さ4,cmのおうぎ形 (2) 半径cm,弧の長さ8,cmのおうぎ形 面積 面積は「9π㎠の半分の「\(\frac{9}{2}\)π㎠」になるね。 4分の一だったら? 3分の2だったら? とにかく、 もとの円の円周や面積を求めれば、 もとの円と比べておうぎ形がどのくらい残っているかによって、 おうぎ形の面積や円周も求めることができるんだね。
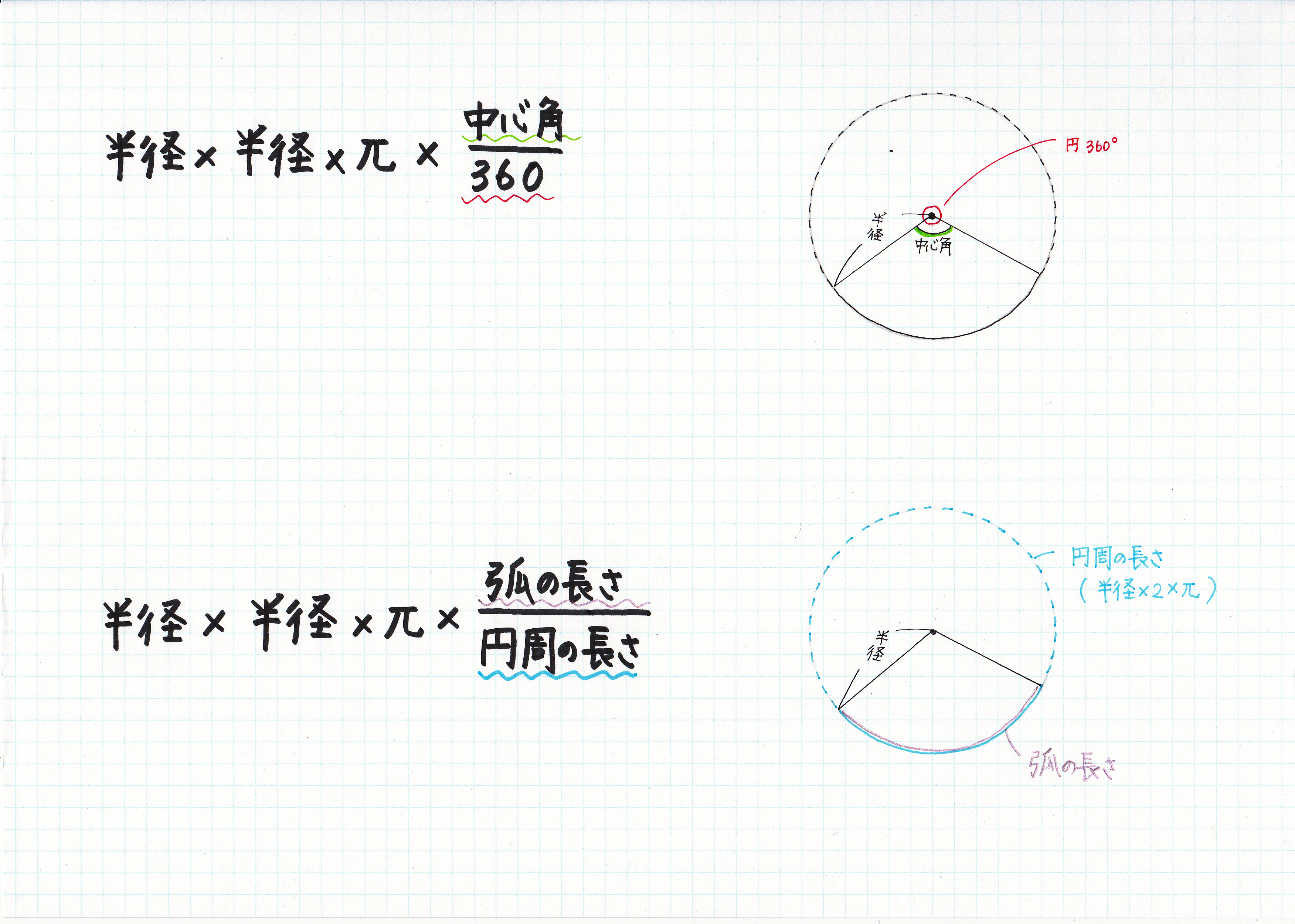
おうぎ形の面積 半径 、中心角 のおうぎ形の面積 は で求めることができる。 先程の弧の長さと同様に円の面積と異なるのは がついている ということです。 これもおうぎ形が 円の面積のどのくらいを占めているのか を表しています。 例えば中心角が入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形 直角二等辺三角形 21年 立体の おうぎ形の公式おうぎ形の面積は、半径をr、面積をS、円周率をπ、中心角をαとすると、S = πr² × α / 360となります。つまり、円周率×半径×半径×中心角÷360です。たとえば、半径3cm、中心角が90度の扇形があったとします。扇形の公式にあてはめるとS = 3×3×π×90/360= 9π/4となります。扇形の




円とおうぎ形 応用 無料で使える中学学習プリント




中1数学 おうぎ形の応用問題 練習編 映像授業のtry It トライイット
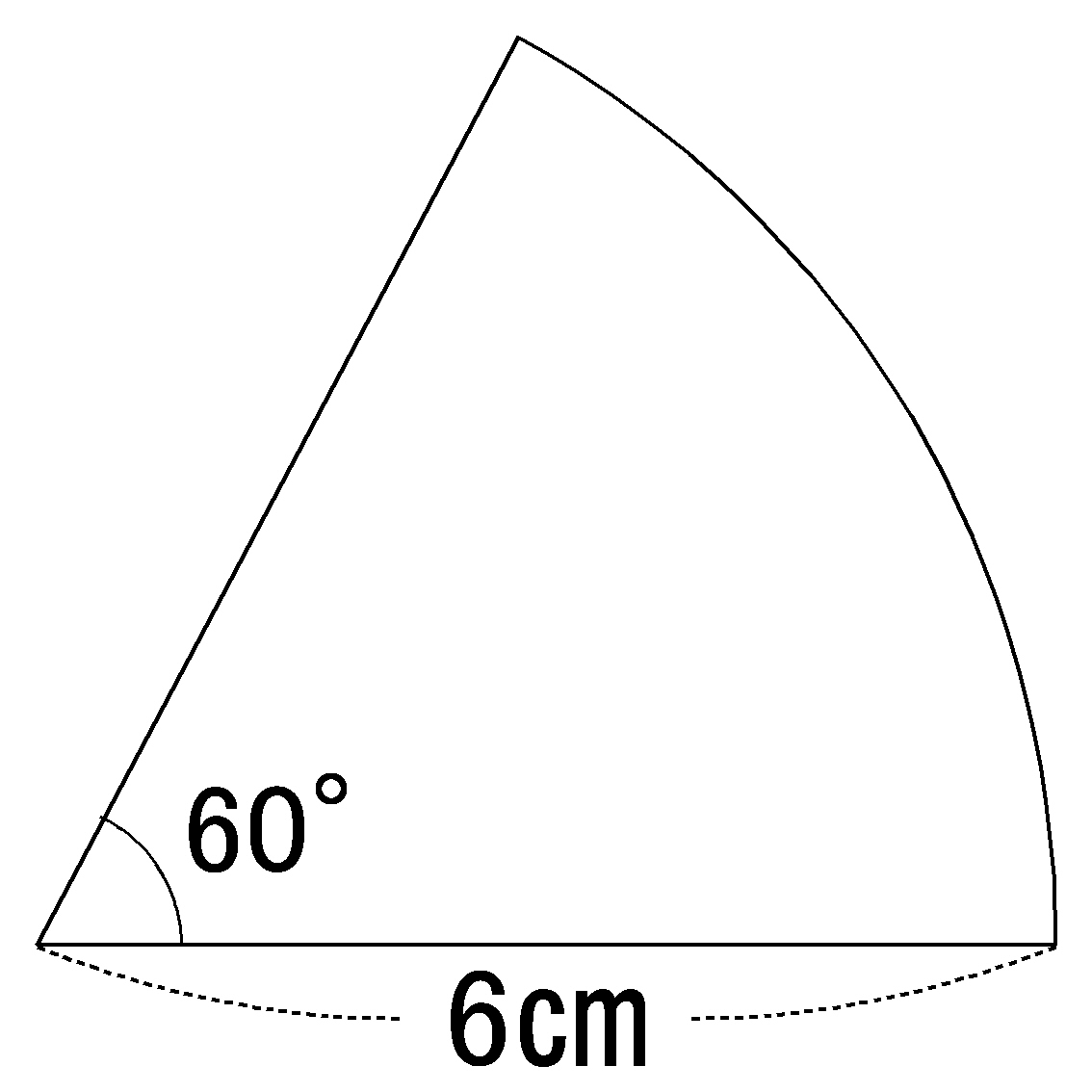
右の図は,円 錐 すい の展開図であり,側面となるおうぎ形は,中心角が135°で面積が ㎝ 2 である。 この円錐の底面となる円の半径の長さを求めなさい。おうぎ形の面積 お う ぎ 形 の 面 積 = 6 × 6 × 314 × 30 ° 360 ° = 36 × 314 × 1 12 = 942 (c m 2)入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 女子校 直角三角形 4年生 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 二等辺三角形 ファイナル 直角二等辺三角形 21年 立体の




教えて下さい お願いします Clear



1
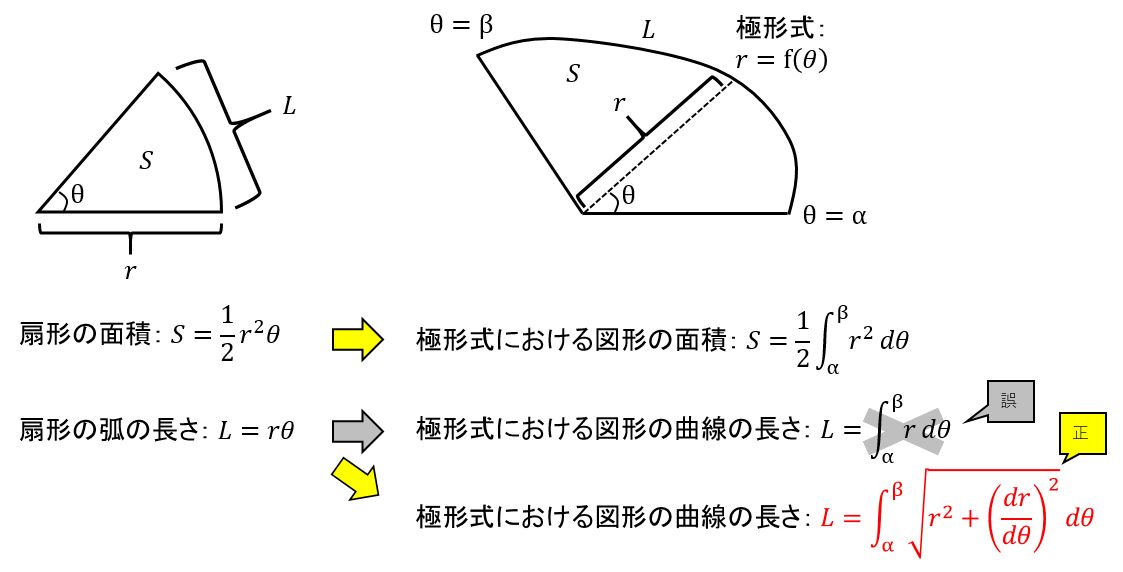
円とおうぎ形⑺ 正三角形が関係する問題 6 6 次の図は、1辺の長さが6㎝の正三角形と半円を組み合わせた図形です。 色のついた部分の面積を求めなさい。ただし円周率は314とします。 もしおうぎ形ではなく円であれば、面積は πr2 π r 2 なので、比で考えると S πr2 = θ 2π S π r 2 = θ 2 π なので、これを S S について解くと S = 1 2r2θ S = 1 2 r 2 θ となります。 もちろんこれでもいいのですが、弧の長さの式を使ってさらに変形することもできよって、おうぎ形の面積と弧の長さは以下のように求めることができます。 お う ぎ 形 の 面 積 中 心 角 お う ぎ 形 の 弧 の 長 さ 中 心 角 お う ぎ 形 の 面 積 π r 2 × 中 心 角 360 ° お う ぎ 形 の 弧 の 長 さ 2 π r × 中 心 角 360



Math 円の問題を解くときに使う3つの技 全体 白 分配法則 移動 働きアリ




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題
おうぎ形(半径と弧、または面積から中心角を出す) 5 5 次の問いに答えよ。 (1) 半径 15 2 ㎝、面積10π㎝ 2 のおうぎ形の弧の長さを求めよ。 (2) 半径5cm,面積2πcm 2 のおうぎ形の弧の長さを求めよ。 (3) 半径7cm,面積42πcm 2 のおうぎ形の弧の長さを求めよ。 おうぎ形の面積 = 半径 × 半径 × π × 中 目次 平面図形の面積の求め方の公式 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 円周=直径×円周率(314)=半径×2×円周率(314) 円の面積=半径×半径×円周率(314) おうぎ形の弧の長さ=円周×中心角/360・おうぎ形の形を実 際に作図してイメ ージさせる。 ・おうぎ形の弧の長 さと面積は中心角 に比例する。 ・おうぎ形の弧の長 さと面積は円の周 の長さと面積に必 要な角度をかける ・(円周率)=円周/直 径 ・おうぎ形の面積は 2通りある



小5の学習ポイント2 円とおうぎ形 前田昌宏の中学受験が楽しくなる算数塾



1
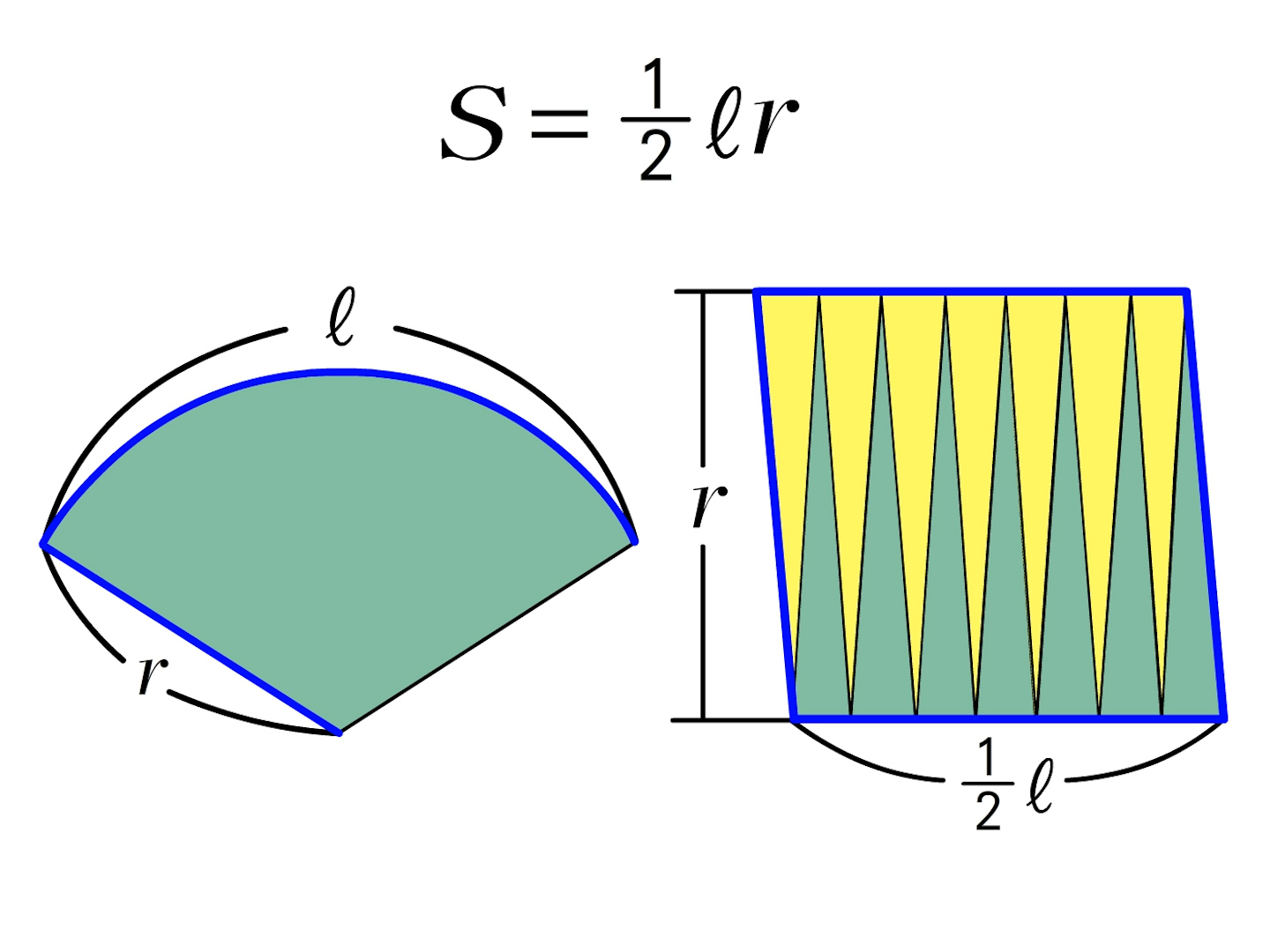
(2) 斜線のついた部分の面積は何㎠ですか。 おうぎ形の面積10×10×314×1 4 =25×314=785(㎠) 10×10-785=215(㎠) 3 次の図はそれぞれ、正方形と円またはおうぎ形を組み合わせた図形です。 (1) 図1の斜線部分の面積の合計は何㎠ですか。面積 同様に扇形の面積 S も中心角の大きさに比例する。 半径 r の円板の面積は πr 2 であるので、中心角が θ のとき = = となる。また θ = l / r より = となる。おうぎ形の面積の求め方1 おうぎ形ABCが存在する時に扇形の面積をSとすると、この面積Sを求める公式は次の (1)式のようになります。 S= 1 2(半径AB)(弧BC) (1) (1) S = 1 2 (半 径 A B) (弧 B C)




おうぎ形 の弧の長さと面積 計算ドリル 問題集 数学fun



5 9cm 8picm Descubre Como Resolverlo En Qanda
正方形の面積は、ひし形の公式によって「6㎝×6㎝×1/2=18㎝2」 正方形の一辺をAとした場合、正方形の面積はA×A=18㎝2 Aは求めるおうぎ形の半径なので、おうぎ形の面積は、A×A×314×90/360 ②よりA×A=18なので、18×314×1/4=1413㎝2 おうぎ形の面積(等積移動系)を求めよ問題のパターン 1 等積移動:同じ面積の所に移動させて計算しやすくする 2 葉っぱ4枚:小さい正方形4つに分ける(正方形の面積×057) 3 補助線+等積移動:補助線を引いて等積移動する 4 ヒポクラテスの三日月 おうぎ形の面積は、 「母線の長さ × 弧の長さ ÷ 2」




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
・おうぎ形の面積の求め方を確認させる。 ・円の面積の求め方,それぞれのおうぎ形は円の 何分の何になるのかを確認させる。 (一斉指導) ・画用紙で作った図を提示しながら,どういう情 報があれば影の部分の面積が解けるのか問いかおうぎ形の面積(分割) 新しい教材 楕円の軌跡(シミレーション) チェバ円変形その2おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 °



よく出題される おうぎ形の部分面積 暁星中学 2012年 改題 これが中学入試に出た図形問題



おうぎ形の問題 パターンを知ろう 苦手な数学を簡単に
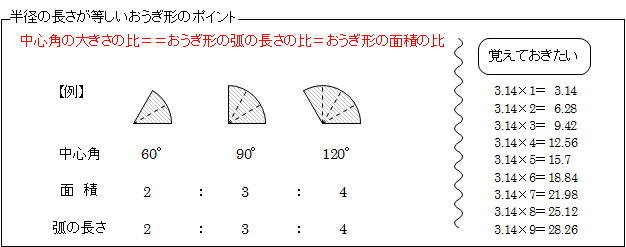
「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方 特殊な問題を除くと、 円周や弧の長さ、円の面積やおうぎ形の面積は 「円周率の倍数 」です。 円周率が314のこの問題では、
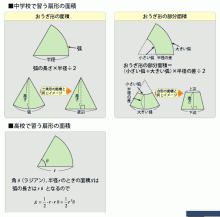



三角形と扇形の面積 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




円とおうぎ形 応用 無料で使える中学学習プリント




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
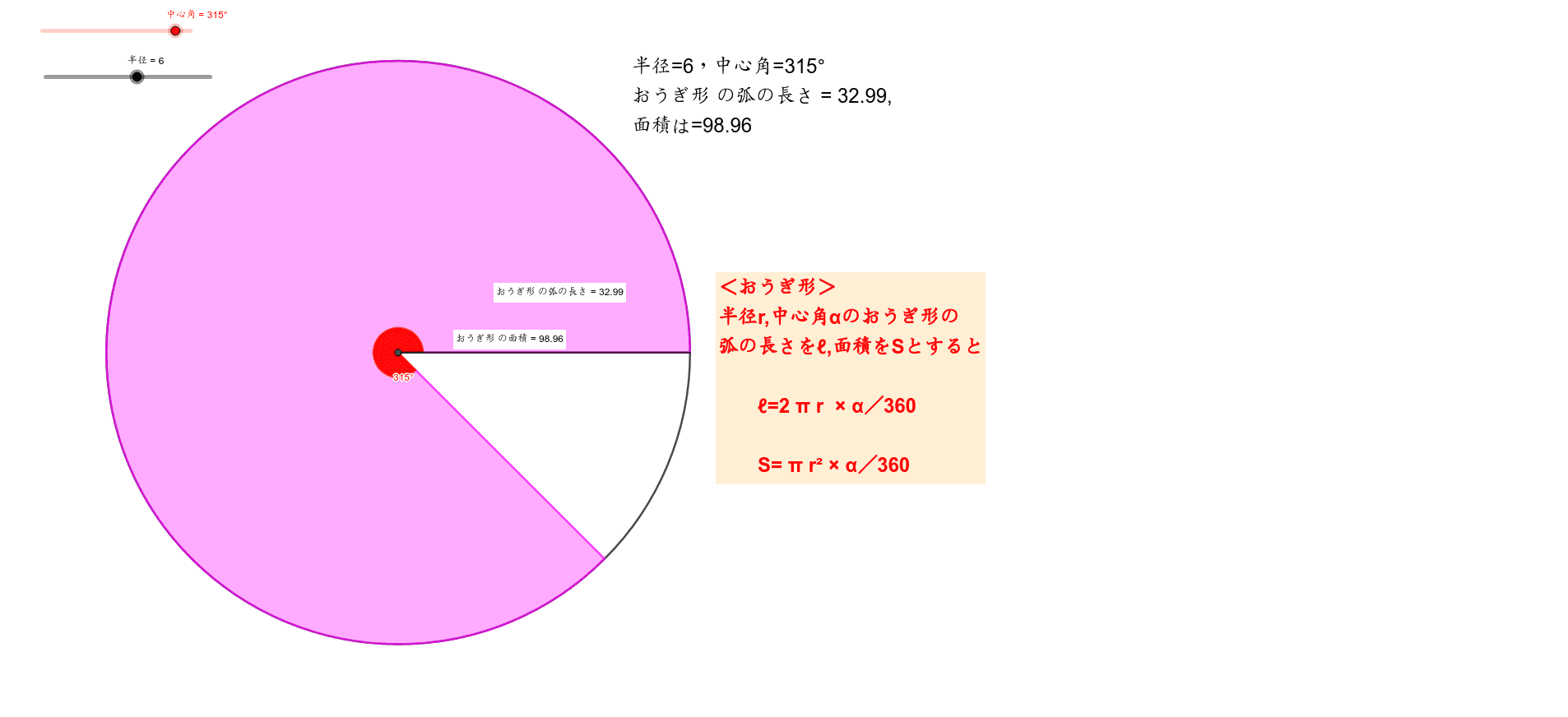



中1 おうぎ形の弧の長さや面積について考えよう Geogebra
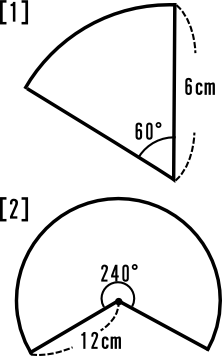



中学1年数学練習問題 円とおうぎ形の面積 円周 孤の長さ 空間図形




おうぎ形の弧の長さと面積の求め方 チーム エン



1




標準 おうぎ形の弧の長さや面積 なかけんの数学ノート




おうぎ形の弧と面積 Youtube



1年 おうぎ形の面積 数学イメージ動画集 大日本図書




算数 本当に 分かる という事 おうぎ形の面積その1 エース学院
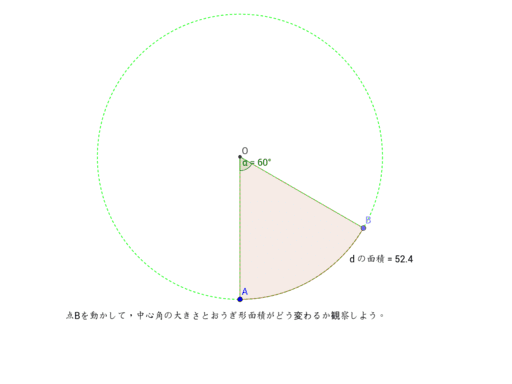



中心角とおうぎ形 Geogebra
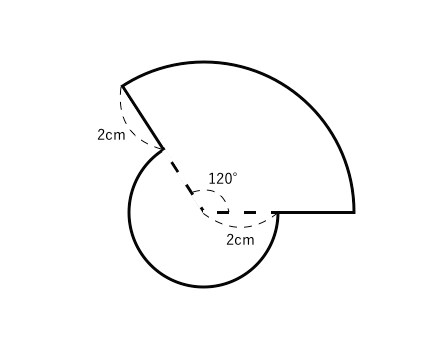



おうぎ形の問題 ちょっと応用編 苦手な数学を簡単に




応用 おうぎ形と正方形の面積 なかけんの数学ノート
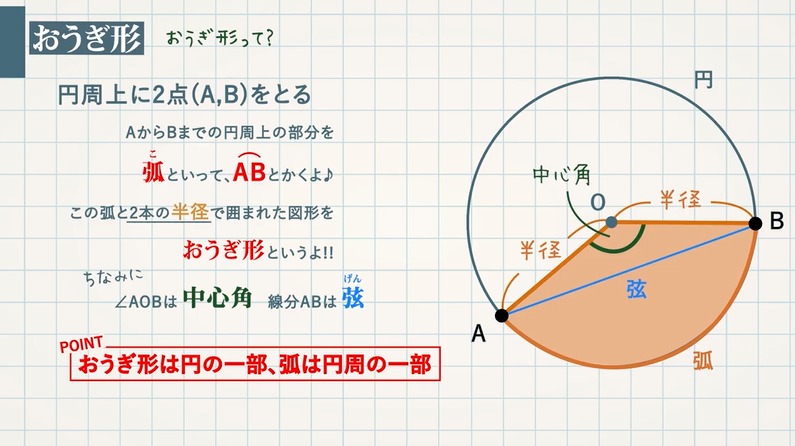



おうぎ形まとめ 弧と面積の求め方 教遊者



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




おうぎ形の面積と弧の長さ Geogebra




おうぎ形面積の超簡単な求め方 合同会社エスキージャパン




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月
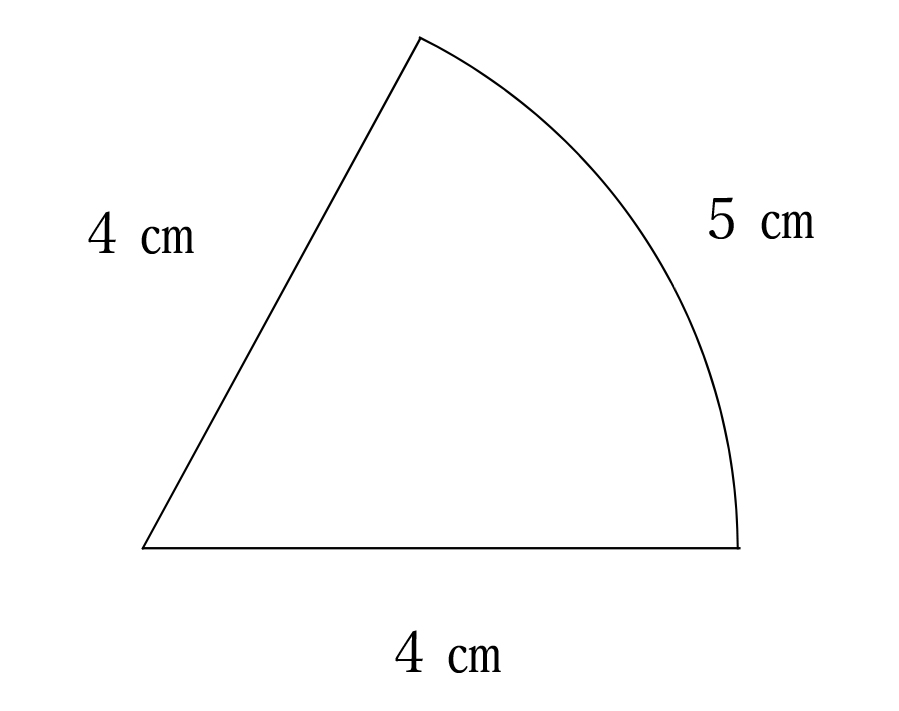



おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




小学校6年生の算数 数学fun 数学 小学校 算数 算数
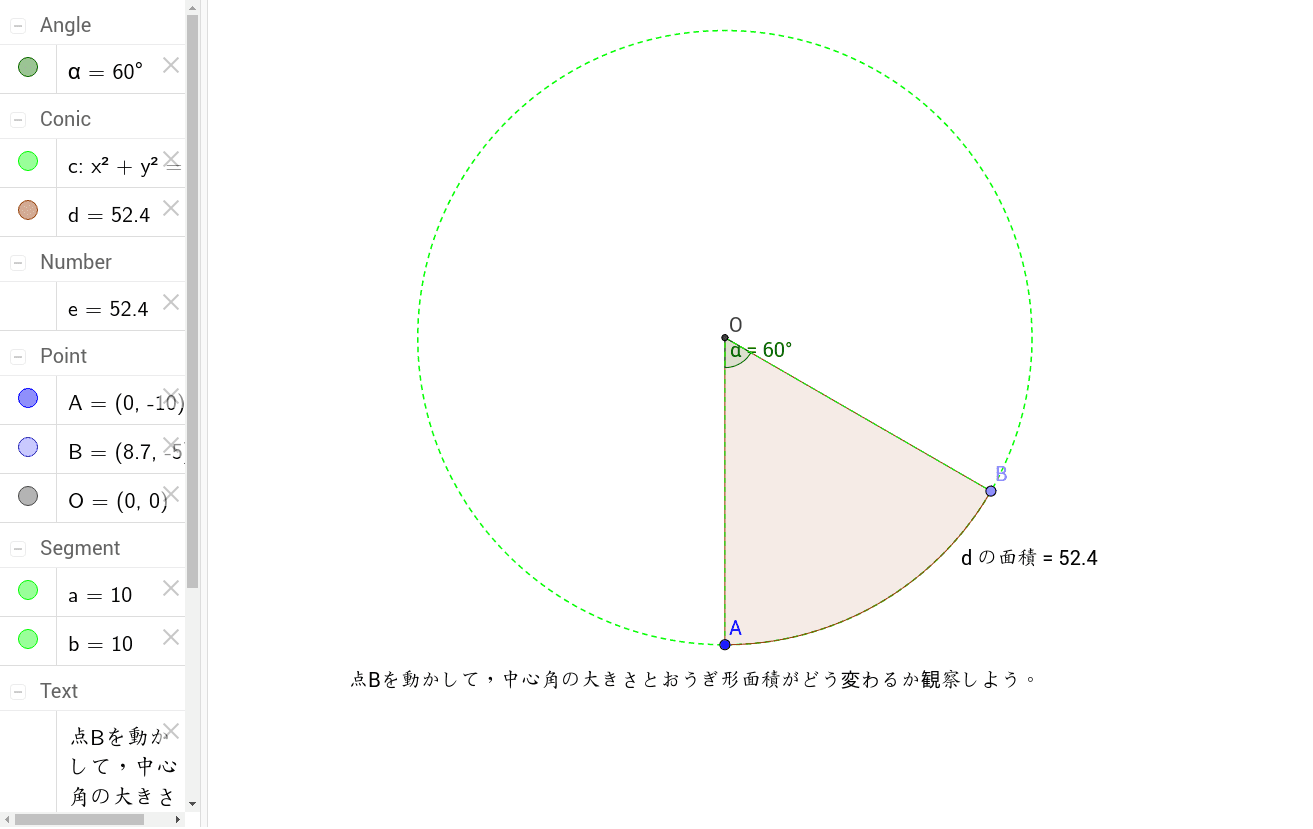



中心角とおうぎ形 Geogebra
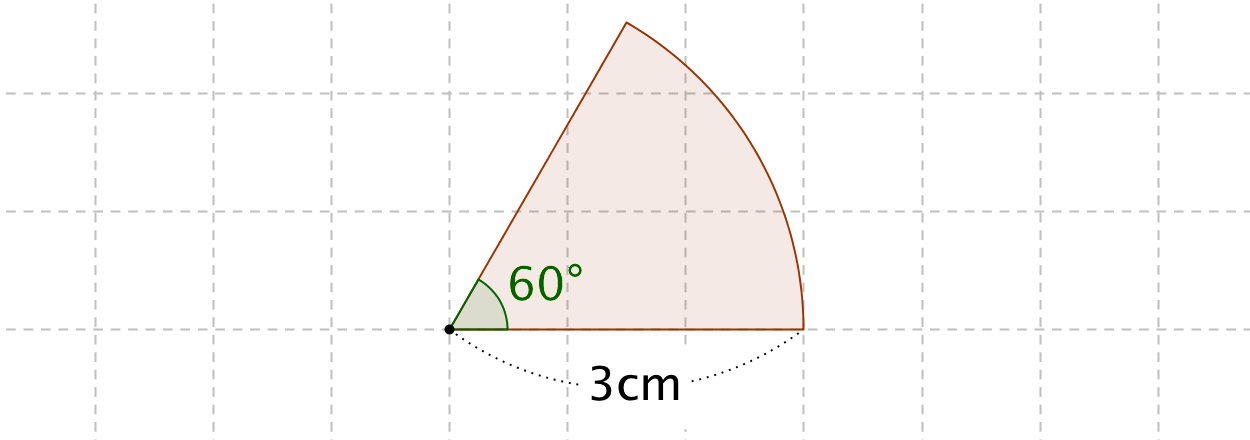



おうぎ形の面積の公式 算数の公式




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
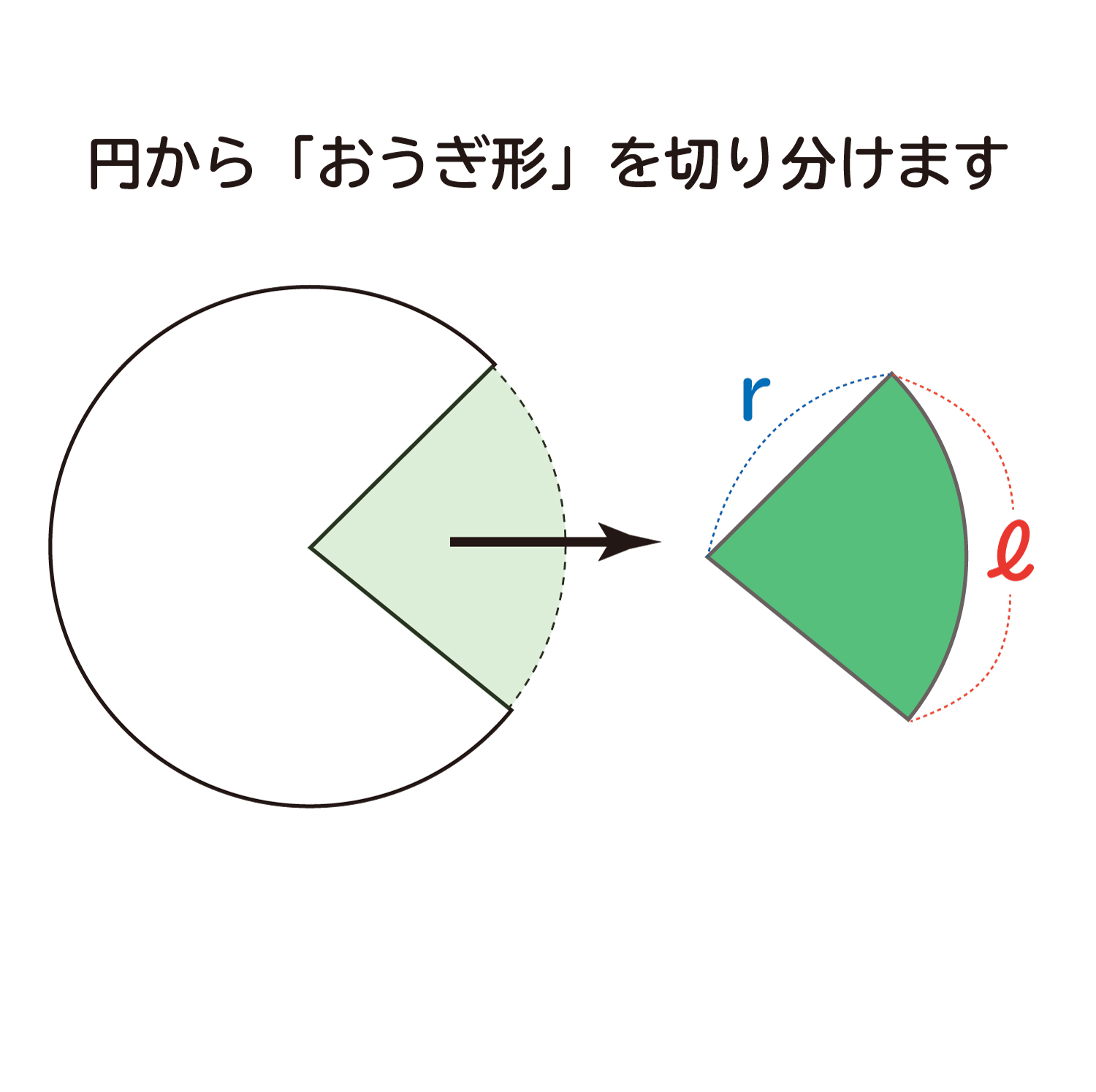



なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア




半円を回転させる面積の問題 プリントを使って自分で解こう



中学入試の図形の問題です 正方形とおうぎ形を組み合わせた以下の図形で Yahoo 知恵袋



円 おうぎ形問題より 60 をさがせ 三角定規 これが中学入試に出た図形問題




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



半円と扇形が重なってる部分の面積の求め方どうやったら良いですか 黒く塗 Yahoo 知恵袋




扇形の面積の求め方 公式と計算例




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ
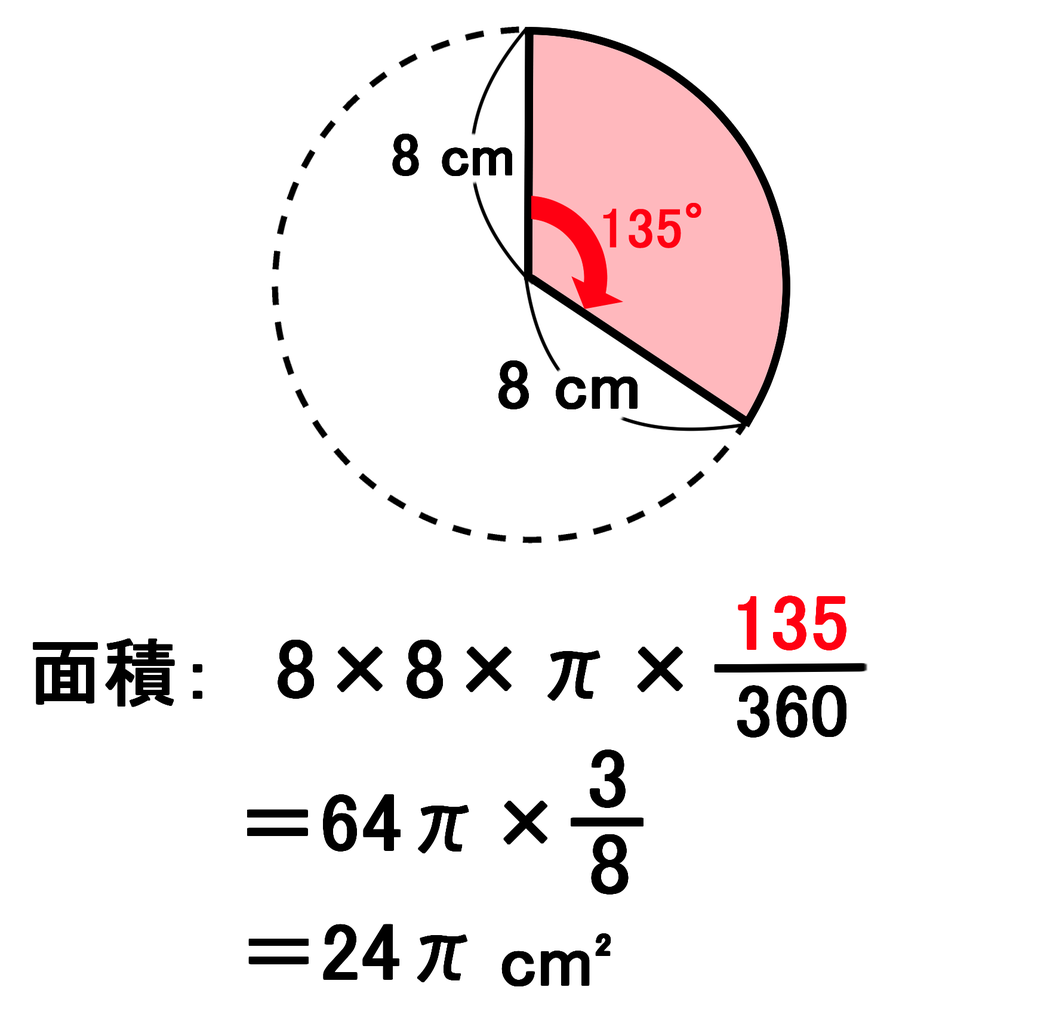



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学



おう ぎ 形 の 面積 求め 方
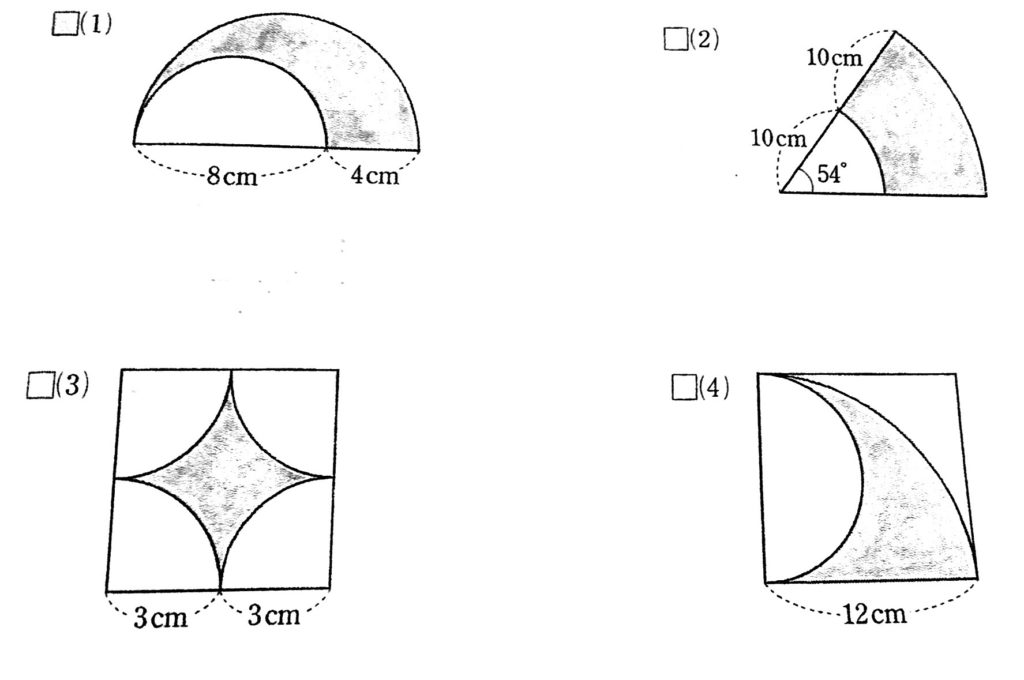



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




数学パズル 意外と悩むおうぎ形の面積問題 ひらめいたらスッキリします 暇つぶしに動画で脳トレ




中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです 今はとに Clear




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




おうぎ形の面積 弧の長さ 数学ノート




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
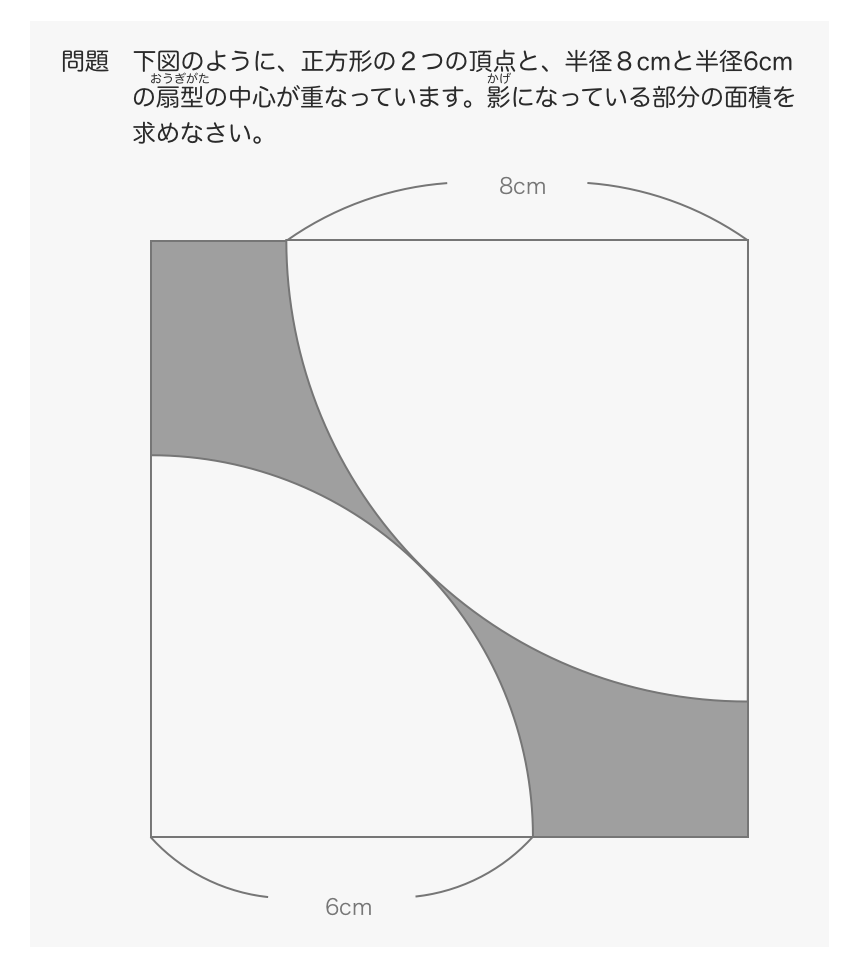



自作教材 円と扇形2 本質と技とコツ カテキョウブログ
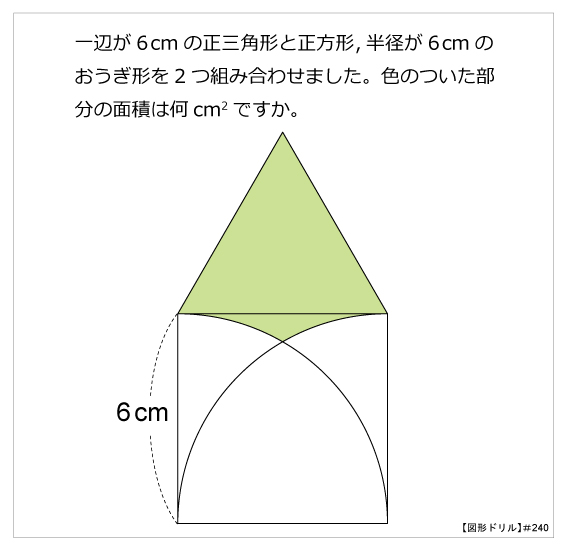



図形ドリル 第240問 正方形と正三角形とおうぎ形 算数星人のweb問題集 中学受験算数の問題に挑戦



モノマナビ研究所




Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう



円とおうぎ形の面積 唇の形 カテキョウブログ



おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方
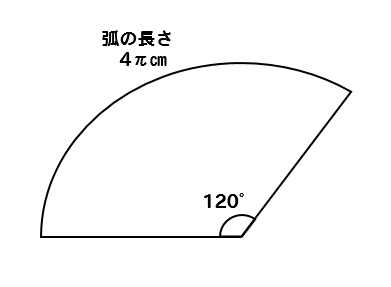



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
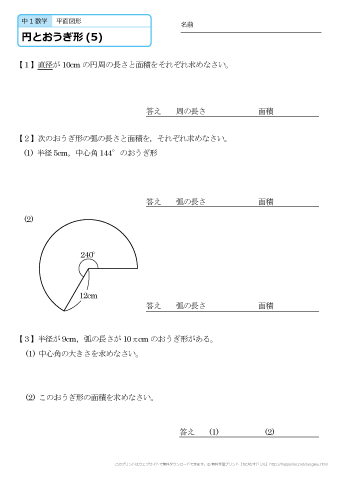



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



高校入試数学 おうぎ形についての公式まとめとその練習問題




標準 おうぎ形と正方形の面積 なかけんの数学ノート




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear



1




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
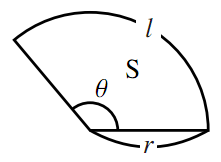



扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
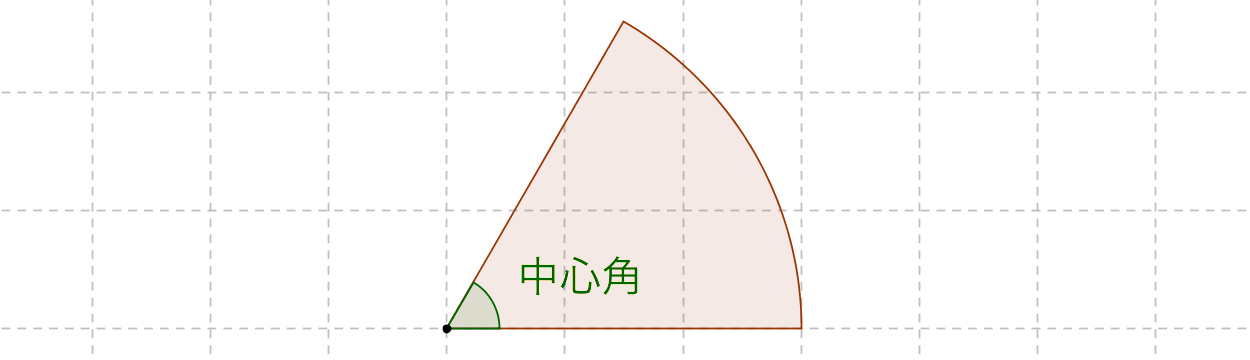



おうぎ形の面積の公式 算数の公式




なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル




おうぎ形の面積 弧度法との関連から眺める 身勝手な主張



5 See How To Solve It At Qanda



みんなの算数オンライン 中学受験 4年 円とおうぎ形 円と面積応用 トレーニング




扇形の面積の求め方 公式と計算例




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




おうぎ形の面積の求め方2つと葉っぱ レンズ 形の面積の求め方3つ 等積移動 中学受験 塾なし の勉強法




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



無料 中1数学 標準問題 解答プリント 138 平面図形5 おうぎ形の弧と面積



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強
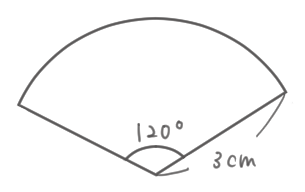



おうぎ形の弧の長さと面積 が苦手でもコレなら分かる 中学1年数学 平面図系 教科書をわかりやすく通訳するサイト




円 扇形 の面積 周や弧の長さの公式 数学fun



おうぎ形の弧と面積 On Vimeo
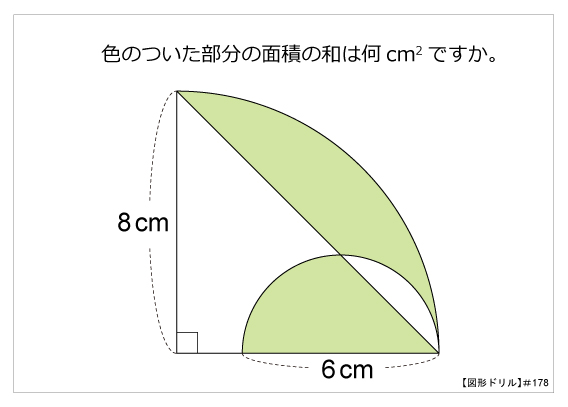



図形ドリル 第178問 おうぎ形の複合図形 算数星人のweb問題集 中学受験算数の問題に挑戦




おうぎ形の中心角の求め方 Youtube




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学
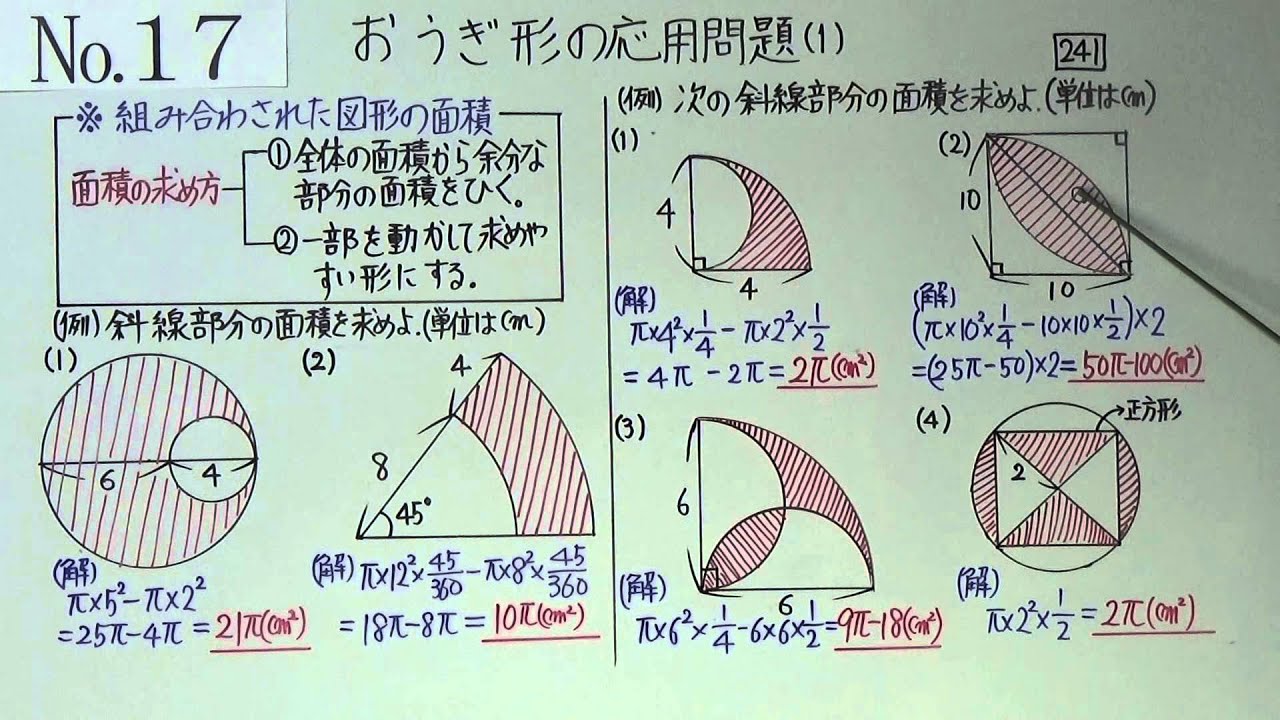



中1 17 2 おうぎ形の応用 1 Youtube




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 2 Youtube



問題93おうぎ形の面積



0 件のコメント:
コメントを投稿