小3算数 1万~1億の数、2~3ケタのわり算・かけ算、ひっ算,分数・小数、4ケタの足し算・引き算,円と球、重さ 例足算,引算、分数、小数、図形ナド より、分数は分数で小2~小6まで一通で学習した方が効率的とお考えの方は、『単元別の小学算数
【人気ダウンロード!】 おうぎ形 面積 145067-おうぎ形 面積
面積を求めよ。 次の問いに答えよ。 半径2cm,弧の長さ3πcmのおうぎ形の面積を求めよ。 半径6㎝、弧の長さ 10 3 π㎝のおうぎ形がある。面積を求めよ。 半径3cm弧の長さ5πcmのおうぎ形の面積を求めよ。 半径9cm,面積9πcm 2 のおうぎ形がある。 中心角を求めよ。 下の図の色の付いた部分の面積を求めなさい。ただし円周率は314する。 解説 下の図のように図形を分けて、考えます。 分けた後の図形の色の付いた部分は4分の1の円の面積(中心角90°のおうぎ形)から直角二等辺三角形の面積を引けば求めることができます。扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を
Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう
おうぎ形 面積
[コンプリート!] 図形の角の大きさ 108266-図形の角の大きさ プリント
(1) 図形の性質に関心をもち,三角形や四角形の角の大きさの和について,筋道を立てて考えようとし ている。 算数への関心・意欲・態度 (2) 三角形の3つの角の大きさの和が180°であることを帰納的に見いだし,四角形の4つの角の大きまた,角については2 本の半直線が作る平面図形としての角を定義し,2 つの辺の開き具合によって形が違うなど,形としての角の概念について基本的なことを学習して きた。第4 学年では,回転による反直線の開きの量としての角を扱っている。また,四角形につ いては,台形,平行四辺形 図形の角の大きさ 5年生 三角形の内角の和が180°であることをもとに、三角形や四角形の示されていない角の大きさを求める問題にチャレンジしていました。

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
図形の角の大きさ プリント
[10000ダウンロード済み√] おうぎ形面積 118986-扇形面積
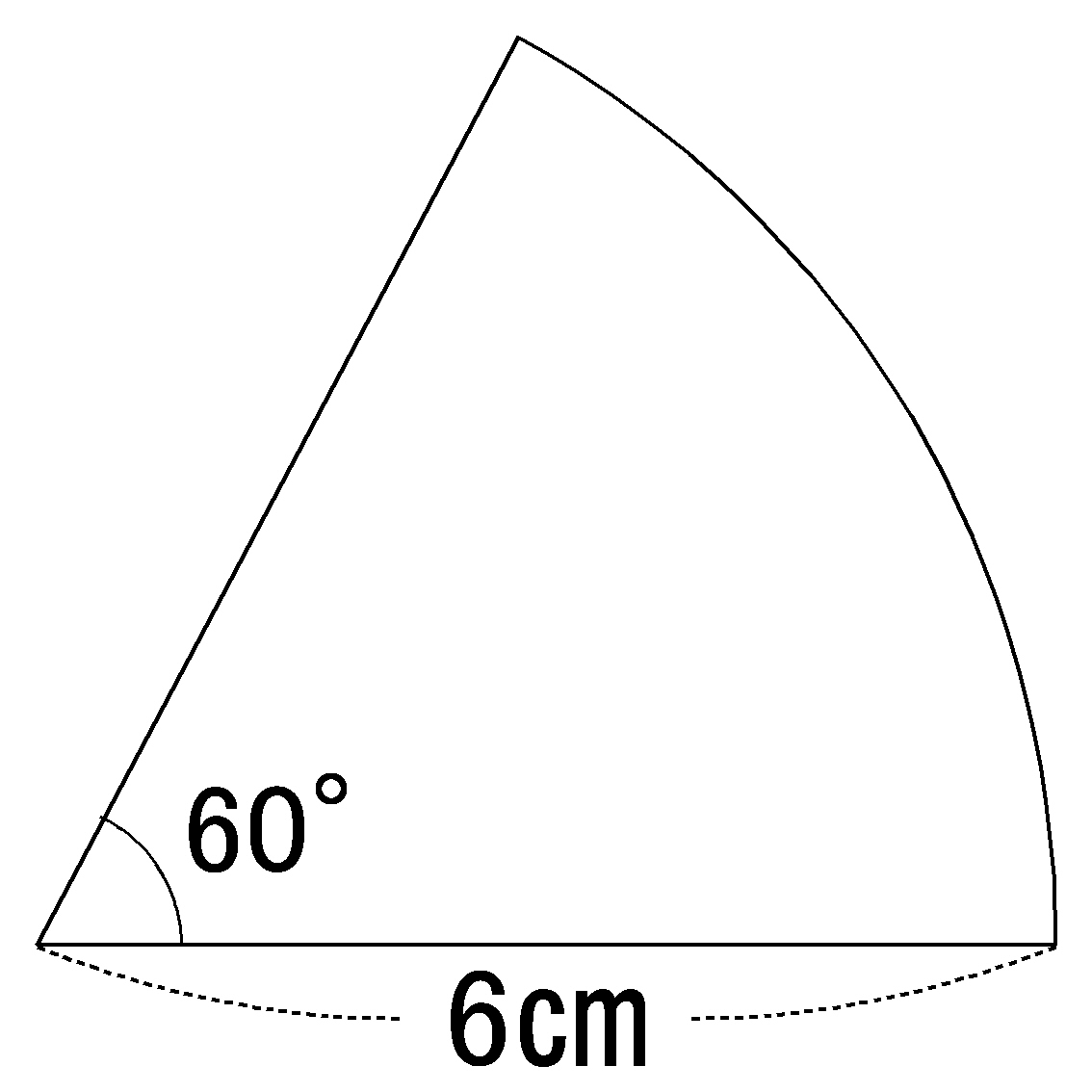
円とおうぎ形⑺ 正三角形が関係する問題 6 6 次の図は、1辺の長さが6㎝の正三角形と半円を組み合わせた図形です。 色のついた部分の面積を求めなさい。ただし円周率は314とします。 おうぎ形を含む図形の面積の難問。 今回は、小学生向けの図形の計量の難問を考えてみます。 上の図の濃く塗られた部分の面積を求めます。 まずは、左の図から。 円を元にして描いた、同じ図形が3つ組み合わせされた図形であることは、すぐに見ておうぎ形の面積の求め方1 おうぎ形ABCが存在する時に扇形の面積をSとすると、この面積Sを求める公式は次の (1)式のようになります。 S= 1 2(半径AB)(弧BC) (1) (1) S = 1 2 ( 半 径 A B) ( 弧 B C) この時の比較として三角形DEFも置いておきます。 三角形の面積を求める公式はもちろん 1 2( 1 2 ( 底辺)() ( 高さ)) となります。 1つ目の面積の求め方はおうぎ形を分割していくことに
Studydoctorおうぎ形の公式と忘れない考え方 中学1年数学 Studydoctor
扇形面積
√完了しました! 四角形の内角の和 証明 586281-四角形の内角の和 証明
2-4-1 星型多角形の内角の和 教材(問題場面) ※m 点とばし星型n 角形の内角の和は180°×(n-2-2m)と表すことができる。 180° 360° 540° 7° 900° 1080° 1260° 1440° 180° 180° 180° 360° 360° 360° 540° 540° 7° 内角の和・外角の和の証明 なぜn角形の内角の和が180°×(n2)となり、外角の和は360°になるのか見ていきましょう。 内角の和について 多角形の内角の和は小学校のときに習ったと思うので復習になります。向かい合う角の和は180° 円に内接する四角形における一番有名な性質です。 180^ {\circ} 180∘ である。 つまり, 性質1の逆も成立します。 つまり, 向かい合う内角の和が 180^ {\circ} 180∘ である四角形は円に内接します。 また,性質1は「外角」を使って
多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
