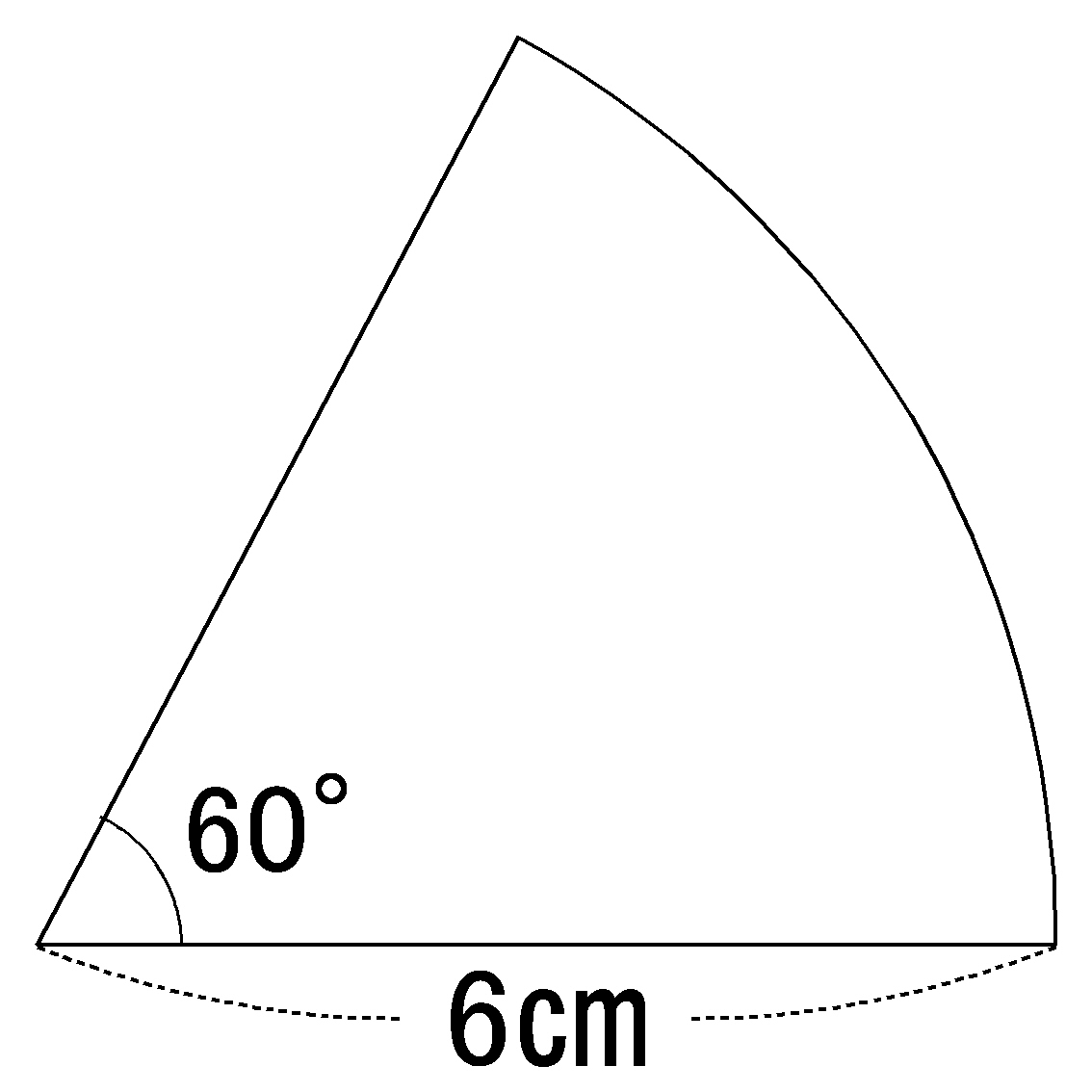
「相似ではない」2つの四角形があります。面積比を求めてください。 高さがhで共通しています。よって面積の値は Aの面積 a×h=ah Bの面積 b×h=bh です。面積比=ahbh=abです。つまり高さの等しい四角形の面積比は「底辺の比率」と等しくなります。これは三角形でも同様です。 ひし形の面積の公式は 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の 4倍 と考えると分かりやすいです。 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の面積は \(高さ×底辺÷2=(たて÷2)×(横÷2)÷2\) a d e ade a d e と四角形 b d e c bdec b d ec の面積比を求める問題も多いです。 また, B C BC BC と D E DE D E が平行の場合は相似な図形の面積比の公式に帰着されます(これも超頻出で
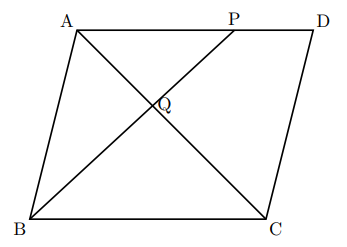
攻略法 平行四辺形と面積 数樂管理人のブログ